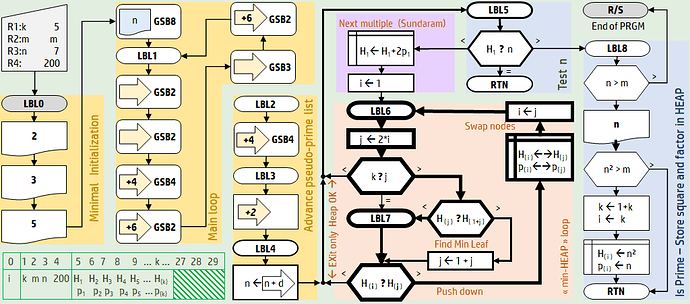
Here’s a marvellous thing, a flowchart by C.Ret as seen on the Silicium forum, which packs a pretty sophisticated prime searching algorithm into the 98 steps of the HP 29C:
I like this notational device:
The thickness of the lines corresponds to the number of repetitions for m = 10,000
This earlier post has a bit of a plan of attack which can serve as orientation.
Before my first computer, I had a TI-57 which was a fairly limited programmable calculator (see also My first programmable calculator) and one of my favourite things was to find prime numbers. The calculator had no printer or permanent storage and no indirect memory access so the only way I could think of to calculate a list of primes was to pack the distances of some consecutive primes into a number. Then I could leave it running for longer before coming back to tabulate the answers. I remember one time a friend visited, noticed the display flickering as it ran, and turned it off and on again, exclaiming that it had gone wrong… which lost me a bit of time.
Anyhow, I was able to fit in a small ‘wheel’ of increments: 4, 2, 4, 2, 4, 6, 2, 6 to skip not just even numbers but also multiples of 3 and 5. And I knew to stop trial divisions at the square root. But that was about my limit of sophistication - the above algorithm goes so far as to manage a data structure of near-primes, as far as I can tell.
(via Thomas Klemm on hpmuseum forum who recommends this online 29C emulator.)
In fact Thomas first offered his own solution, an improvement on the approach from the October 1980 BYTE as blogged by Jurgen Keller, and then explained this program by C.Ret:
Instead of checking if a number is divisible by a prime the odd multiples of the primes are calculated starting from the square of the prime.
For 7 that would be: 49, 63, 77, 91, 105, …
Or for 11 that would be: 121, 143, 165, 187, …Of course we can’t keep all of them since we have only 30 registers.
But we don’t have to. All we need is keeping the smallest among them.These numbers are kept in a min-heap and thus we only have to check the smallest of them which is in register 5.
If the number is smaller it is a prime.
If they are the same it’s not a prime and we can proceed with the next number.
If it is bigger we have to update the multiples of primes in the min-heap.And while doing so make sure it’s still a min-heap.
Thus some of the elements have to be rearranged.