Yes, exactly, it’s a classic display hack.
Not knowing who did it (compare Snowflake) or when it was done (compare the Minskytron) is some of a tradition. 
A PDP-1 version may need a sine/cosine lookup table, though. Unless we can somehow translate this to Minsky’s fast circles,
Regarding fast circles, here’s Minsky’s version, assuming an origin at the center (0/0)
(“times epsilon” is actually a division by shifts):
NEW X = OLD X – epsilon * OLD Y
NEW Y = OLD Y + epsilon * NEW X
This is an accidental variation of
NEW X = OLD X – epsilon * OLD Y
NEW Y = OLD Y + epsilon * OLD X
where we substitute epsilon for sin(θ) and 1 for cos(θ) in the full formula
NEW X = X * cos(θ) - Y * sin(θ)
NEW Y = X * sin(θ) + Y * cos(θ)
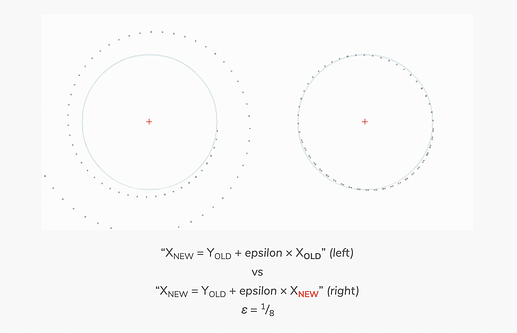
Notably, this sped up version results not in a circle, but in a spiral. To see, why this is, consider the determinant of the generating matrix, which must be 1 for any conic to meet, where it started, but is off by ε². Meaning, it’s spiraling out. The accidental variant evens this out, resulting in a determinant of 1.0, but it’s a actually a fat ellipse rotated by 45°, which is very close to a circle.
(Visualization from a blog post on the Minskytron, I’ve in writing for what is now ages. Ideal circle in blue. Both approximations improve with deminishing epsilon.)
We could manipulate this by either changing epsilon (meaning, it’s not symmetrical for x and y), or adding to the either coordinate in the process.
So, maybe there could be something done, based on
x = x - (y >> sy)
x = y + (x >> sx)
by manipulating either part inside of one of the parenthetical expressions…
If this works out, we should get a significant speed improvement for any older systems.