Investigating Basic floating point accuracy (and finding a bug)

Software
1

It’s one of my hobbies, really, to worry about accuracy and to try to find small differences. For example
PRINT 7E7+1234-7E7
will give me 1234 when I’m using a Basic with 5 byte floats, but 1232 when using 4 byte floats. That’s more or less as expected, although I might have tried harder to see the effects of rounding.

But I’ve become puzzled by something. When are two things not equal, but their difference is zero? I didn’t expect that - specifically in the MS Basic found on the PET, as seen in @NoLand’s online emulation. I wonder if I’m doing something wrong.

image
image690×534 54.3 KB

Here’s the program: the idea is to find pairs of numbers which illustrate the limited accuracy of square roots.

10 FOR I=2 TO 9
20 FOR J=2 TO I
30 IF SQR(J*I)=SQR(J)*SQR(I) GOTO 40
35 PRINT I,J,SQR(J*I)-SQR(J)*SQR(I)
40 NEXT
50 NEXT

The results on a Beeb are much more as expected - if the two expressions are unequal, their difference is not zero.

image
image787×568 62.2 KB

2 Likes
2

I ran in to something similar on Pi Day (3/14) when I did an experiment calculating Pi iteratively.

I ran the same program on as many of my vintage machines as possible (and I just remember that I didn’t run it on my pocket computers, darn).

The non-Commodore machines needed many more iterations before the value of Pi stabilized (i.e. reached the max of the machine and I was just adding 0).

My understanding is that Commodore wanted BASIC to fit in a much smaller ROM area, so the floating point routines were purposely kept low precision. Good enough for most business, but not enough for scientific processing.

3

Puh! (Traditional Austrian form for “phew”.) I’d really had to have a look at what the BASIC implementation is doing.
In principle, number representation (in stored variables!) is 4 byte mantissa an one byte exponent, which is shifted for a bias of 127 and the sign is encoded in the first byte of the mantissa.

So, given an exponent e and a mantissa m0…m3:

m = (m0 | 0x80) * 2^-8 + m1 * 2^-16 + m2 * 2^-24 + m3  * 2^-32
r = m * 2^(e-0x80))
sign = (m0 & 0x80)? '-':'+'

The output representation is in common notation for 0.01 < r < 999999999 with up to 9 digits, otherwise exponent representation with up to 8 fractional digits and exponent of 10.

(Also, there are no real integers. Integers are stored in 2 byte format — for simple variables still using 5 bytes, like floats, only in arrays they are packed into to bytes —, but are converted to floating point on use. They actually stripped the integer code from the usual MS BASIC, in order to fit the code into the available ROM.)

But this doesn’t tell us anything about the square root algorithm, which is probably the true culprit…

4

Maybe I need to clarify my specific point of confusion: the program should never print a zero in the third column, I would think, because the two things being subtracted have been tested and found not equal.

5

FWIW: Using single precision (ie. 32-bit/4 byte) IEEE 754 arithmetic (implemented in my BCPL system), I get the same error for

  a := 7e7
  b := 1234.0

  writef ("Ed test: %9.5d*n", FIX (a #+ b #- a))

Which results in: 1232.

Commodore Basic, as compiled from the freely available sources give me the right result though:

* /cbm2
### COMMODORE BASIC ###

 29183 BYTES FREE
READY.
PRINT 7E7+1234-7E7

 1234 

READY.

EhBASIC - another Microsoft derived BASIC gives the same error though:

*/ehbasic

65C02 Enhanced BASIC Version 2.22p5C Ruby
 [C]old/[W]arm start? 
29183 Bytes free
Ready

PRINT 7E7+1234-7E7
 1232

Ready

I’d need to investigate the assembly time options on the cbm2 BASIC I’m using though - checked and it is using 5 byte floats. EhBASIC uses 4 byte floats.

Acornsoft Comal gives the correct result but it would not surprise me if it uses the same code inside BBC Basic.

My theory about printing zero when they’re not equal is simply that the print routine can’t print numbers with absolute precision.

FP accuracy and rounding has always been a thing (we had several lectures on it at uni) and I remember at school there was a calculator test which was essentially

  asin (acos (atan (tan (cos (sin (47)))))

My own old school calculator (Imperial 99T) gives 40.02… as a result, but interestingly, if I put the calculator into radians mode, then do the test with 47 expressed in radians then the result is more accurate (to 6 significant digits) but not exact so all those continued converts to radians and back to degrees causes significant loss…

-Gordon

2 Likes
6

Running the short program,

10 I=2:J=3
20 A=SQR(J*I):B=SQR(J)*SQR(I)
30 C=A-B

we get the following variables in memory (compare above for the representation)::

0432  49 00               I
0434  82 00 00 00 00      =  2
0439  4A 00               J
043B  82 40 00 00 00      =  3
0440  41 00               A
0442  82 1C C4 70 A1      =  2.44948974
0447  42 00               B
0449  82 1C C4 70 A1      =  2.44948974
044E  43 00               C
0450  00 00 00 00 00      =  0

Mind that the difference C is actually zero, while the pair (2,3) does print in the program.
So there’s certainly something (a supposedly correcting step) happening, when a variable is stored.

However, modifying the program to use a variable for the difference, we get

LIST

 10 FOR I=2 TO 9
 20 FOR J=2 TO I
 30 D=SQR(J*I)-SQR(J)*SQR(I):IF D=0 GOTO 40
 35 PRINT I,J,D
 40 NEXT
 50 NEXT
READY.

RUN
 7         7        -2.73576006E-09
 8         7         1.99361239E-09

Actuall, the correction seems to be happening, when there is a result, compare this version with a comparison to zero:

 10 FOR I=2 TO 9
 20 FOR J=2 TO I
 30 IF SQR(J*I)-SQR(J)*SQR(I)=0 GOTO 40
 35 PRINT I,J,SQR(J*I)-SQR(J)*SQR(I)
 40 NEXT
 50 NEXT
READY.
RUN
 7         7        -2.73576006E-09
 8         7         1.99361239E-09

Conclusion: zero outside an expression is not not necessarily zero inside of an expression.

7

Interesting - feels like a bug in detecting equality between two floating point expressions. I tried Coco extended basic - also a 5 byte MS basic, but for 6809 - and that didn’t fail. I suppose the existing disassemblies of 6502 MSBasic will enlighten us, if we study them.

Edit: BTW, if you write “text” (four letters) after opening a block code quote with triple backticks, it turns off unwelcome colourisation.

1 Like
8

That actually works! Thank you!

Just to try out this newly found toy again :slight_smile: , I thought it may be interesting to evealuate this on a term versus factor basis.

Using 0 + SQR(J*I) = 0 + SQR(J) * SQR(I) we still get the same error-correcting error:

 10 FORI=2 TO 9
 20 FOR J=2 TO I
 30 IF 0+SQR(J*I)=0+SQR(J)*SQR(I) GOTO 40
 35 PRINT I,J,SQR(J*I)-SQR(J)*SQR(I)
 40 NEXT
 50 NEXT

RUN
 3         2         0
 3         3         0
 5         5         0
 6         5         0
 7         5         0
 7         7        -2.73576006E-09
 8         4         0
 8         7         1.99361239E-09
 9         2         0
 9         3         0
 9         4         0
 9         6         0
 9         9         0

I don’t think that this is a bug in the floating point routine, but rather by design, in order to provide pretty results. The bug is really how the rounding routine is employed, or not employed, when we do a comparison. If we compare an expression to zero, it will be rounded, but if we compare two complex expressions, there is no rounding.
It somehow makes sense, but as always with smart code, there will be edge-cases. And you have found one of them!

9

Type coercion is always interesting, in any languages.

I know that in some higher level language, the compiler would take something like “int + float” and try to do something intelligent about that since they are different types. Usually, it would convert the int to a float, then do the addition. The result would be coerced depending on the type of variable that was receiving the result.

I’m wondering if this variation of BASIC is coercing the result to an int, thereby removing the decimal places.

10

I guess not, since Commodore BASIC doesn’t feature integer arithmetic. It actually lacks any integer code and variables are just coerced to integer. (Because of this, in contrast to any other BASICs, using integer variables is actually slower than using floating point variables only.)

So, I suppose, it’s rather a “smart” correction algorithm for pretty results. However, you can be only that smart on a 1MHz 8-bit CPU, especially, when speed matters and you have to fit your entire OS and BASIC into a few KB of ROM…

It may be interesting to run this on a C128 in C128 mode, which features a much revised and advanced version of BASIC (BASIC 7.0).

11

For grins, I ran this program - with and without the “0+” in the “if” statement on my TRS-80 PC-2 and in GWBASIC on my NuXT (NEC V20).

The “0+” had no impact on the results. The only difference between the results on both systems is that the PC-2, designed to be more of a calculator, had higher precision. So the differences were xE-11 as opposed to GWBASIC which was xE-07.

1 Like
12

This gives me an idea: I’ll try to run this later on my Olivetti M-10 (much the same BASIC as TRS-80 Model 100) and the NEC PC 8201A, which features a revised version of this BASIC, which is adjusted to better match NEC’s NU BASIC. Both are essentially the same hardware platform as the TRS-80 Model 100.
(I think, contrary to common belief, which tends to regard them as clones of the Model 100, the NEC version was actually the first one to market.)

Both are very complete in their MS BASIC implementation, featuring both short and long inter code. (There’s actually a difference, as one, I believe, the NEC, defaults to doubles, while the other one defaults to short integers.) Also, if this fails, as well, we can blame Bill Gates, as this was famously the last BASIC, he personally worked on. :slight_smile:

1 Like
13

In terms of explicable mechanisms, I’m imagining there’s some kind of floating point accumulator with an extra guard byte, which will be rounded into the result if and when the accumulator is written to a variable, and somehow the comparison for equality is taking these guard bits into consideration. But in such a way that if we actually perform a subtraction, we do get zero. And this seems like an odd combination of possibilities.

14

My TRS-80 Model 102 shows no difference with and without the “0+”.

But it does have higher precision with xE-13 for most values. But I did get more 0 values.

1 Like
15

As far, as I remember, the floating point accumulator has actually a 5-byte mantissa (where stored variables have 4). I’m just not sure, if this provides extra precisson or if this is just a runtime optimization. – Another thing to look up (best in the ROM).
Notably, there are two floating pointing accumulators and these will be used for the comparison. But this doesn’t explain, yet, why the comparison to zero works as expected, as this will be done by the same mechanism. There must be more to this.

Just an idea, is there a difference with simple values that are directly parsed from BASIC text in RAM? As it turns out: no, it’s the same as with literal zero and with an expression resulting in zero.

10 FOR I=2 TO 9
20 FOR J=2 TO I
30 IF SQR(J*I)-SQR(J)*SQR(I)=1.5-1.5 GOTO 40
35 PRINT I,J,SQR(J*I)-SQR(J)*SQR(I)
40 NEXT
50 NEXT

RUN
 7         7        -2.73576006E-09
 8         7         1.99361239E-09
16

I’ve found a potential culprit: There’s a ROM routine “ZEROISE”, which puts zero into the floating point accumulator (FAC), whenever the exponent is zero. This will be called for result normalization. It may well be that this is not called in the case of “SQR(J*I) = SQR(J)*SQR(I)” and the comparison runs over the full 6 bytes of the FACs, while the result is “zeroised” in other cases. ZEROISE will surely be called, when we put the result in a variable or print it.

(BTW, the 6-byte floating point accumulator format just extracts the sign into an extra byte and conversely normalizes the first byte of the mantissa, so this shouldn’t have more precision than the 5-byte storage format.)

Which poses the question, why is this different?
(It’s not about directly comparing results of a built-in function, since — as we’ve seen — it’s the same when we add a factor like zero or 1.5 to each side. Is the SQR() routine expected to have called this already, as it exits, but doesn’t? This seems to be the most likely scenario, at the moment.)

Update: Ah, ZEROISE only applies to FAC#1, which may explain a lot, if one of the results in this comparison always remains in FAC#2.

1 Like
17

PS: I’ve always toyed with the idea of adding a trace to the emulator to investigate such cases. But 1sec of runtime at 1MHz will result in a log of about 300,000 lines in average, which seems a bit unwieldy, not to say, useless. (It may just hog the browser’s memory with little worth otherwise.) As may be single-stepping through BASIC execution.
Is there any worth to this?

One way I could think of how this may become manageable is tagging important ROM locations (like entry points to routines) and tracing only these. But this would mean tagging 3 different ROM versions (and, with a potential upgrade for the business keyboard even 4) + a cross-reference for what any of these tags means. As far as I know, no such reference exists (in a processable format).
If there are any, or, if anyone is willing to produce such a reference, please let me know.

1 Like
18

Great sleuthing! I was wondering what combination of tracing and single-stepping might be able to narrow down what’s going on. Is this problem in all flavours of MS’ 6502 Basic, I wonder, or did it get fixed? (Of course, failing to reproduce the problem doesn’t mean it’s fixed. So maybe it’s still there, even in the 6809 version…)

19

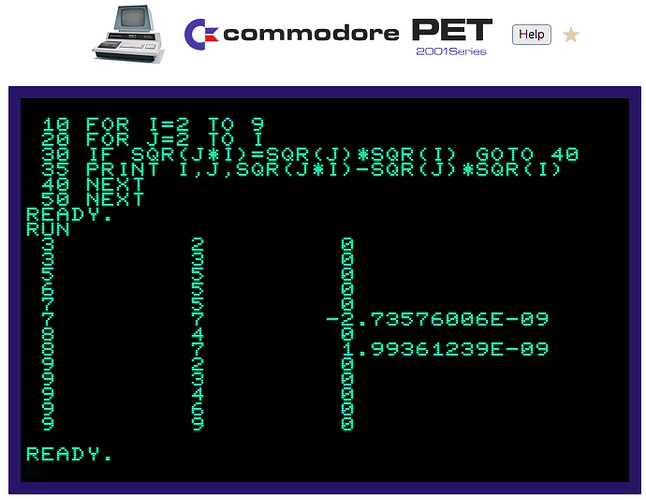
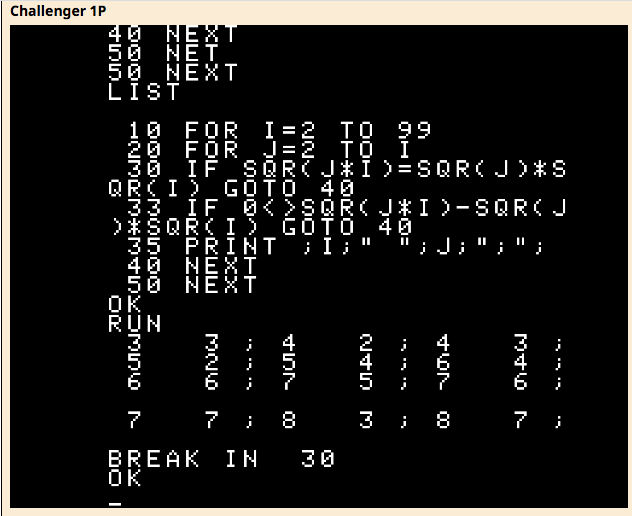
According to the book, where everything I can’t find anything about and eventually go to find out on my own eventually turns out to have been written already (even, if I failed to identify it in the first place), “Programming the PET/CBM” by Raeto West, the Apple II Basic is mostly identical in its arithmetic parts.

Regarding whether this ever got fixed, it’s the same with Commodore BASIC 4.0 (the one that the VIC and C64 never got).
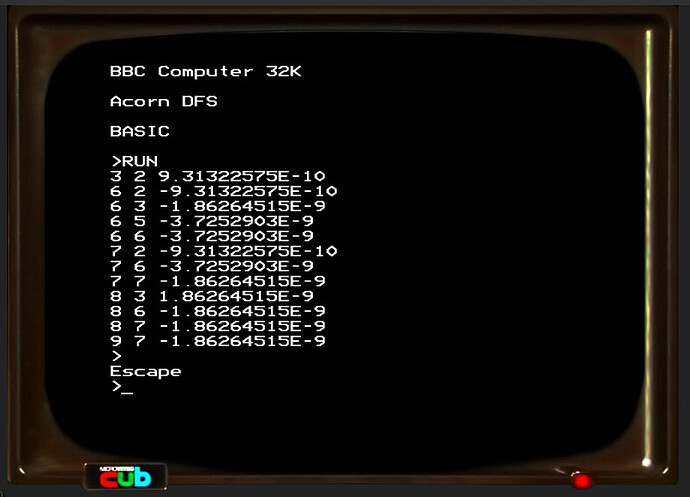
The next big iteration was BASIC 7.0, found on the C128 in C128 mode, which in turn is based on BASIC 3.5 found on the C16/116 and the Plus/4. (BASIC 3.5, in turn, is a descendant of BASIC 2.0, skipping the 4.0 iteration of the later PETs. — This complex family saga may be worth a TV series.) This is said to have some bug fixes. But, as I have no experience with any of this, I just don’t know.

Then, there’s the question of whether this is a bug or not. The routine is designed to work on FAC#1 and this alone. Keeping both results in the two FACs is a sensible shortcut, compared to the alternative of shuffling those 12 bits around in order to “zeroise” the second result. As far as I can see, this is the only edge case, where this would matter. Is it worth to slow down all other operations for this?
(The machines running BASIC 3.5 and BASIC 7.0 run all at 1.67 or 2MHz, so it may have been worth fixing there, as the resulting overhead doesn’t matter that much.)

Having said that, from a functional perspective, this is, of course, a nasty bug. But this is MS and not, say, HP, and their perspective on this may have been different. There were trade-offs to be made, all the time, and business-aspects certainly were a major argument.

What I could think of would be having a list of all the relevant ROM routine entry points and tracing those with their tag name (common label) and a conventional CPU trace. Having relevant context (like the FAC involved, or filename buffers and the like) listed along this would be a nice-to-have. This should reduce the log to about 1% of a complete CPU trace (these are larger blocks and we’re skipping all the loops) and carry all information for following the path, the ROM code takes. But this involves quite an effort for what is probably of limited interest, especially, as there aren’t any (detailed) lists of such labels readily available. It may be interesting for a C64 emulation, though, where there is just a single ROM version and lots of people toying with this.

20

BTW I checked the Ohio Challenger 1P with its 4 byte MS Basic, and it has similar problems, for example with pairs 3,3 and 4,2 and 4,3. (JS emulator here)

image
image632×516 16 KB

That was running this program

10 FOR I=2 TO 99
20 FOR J=2 TO I
30 IF SQR(J*I)=SQR(J)*SQR(I) GOTO 40
33 IF 0<>SQR(J*I)-SQR(J)*SQR(I) GOTO 40
35 PRINT ;I;" ";J;";";
40 NEXT
50 NEXT

An emulated Beeb produced no output for this program, likewise a CoCo2 running extended basic, which is what I’d expect of a correct Basic interpreter - this isn’t about floating point accuracy or even runtime efficiency, I think, it’s just correctness. The square roots are in this case a convenient way to produce interesting floats.

Also just to note, I used your Basic program entry page for PET here and your nearby Beeb page here.