Was GOSUB stack-based in early BASIC interpreters? Was it possible to arrange for automatic (in the C language sense) variables?
GOSUB was surely stack-based, although not necessarily using the CPU’s own stack, if indeed it has one. Microsoft’s Basic didn’t have local variables, whereas Acorn’s BBC Basic did (in PROCs, not in GOSUBs.) But there were very many Basic implementations, so there might well be others which did.
Bear in mind (as an incidental point) that the 6502’s stack, in particular, is rather small. It’s not common to use it much for passing parameters. BBC Basic on the 6502 has a software-managed stack for these purposes. However, the 6502 is only one CPU of very many. Most have a full size stack, although a few don’t have a stack, or have a very small fixed size stack only for return addresses - in these cases, a software managed stack would be needed.
I know that a pascal compiler, was boot strapped using basic into P-code. That was on a 8080.
Byte 1978 ish.
Yes, it’s somewhat a question of definition: for full recursion, you’d probably need stack frames, i.e., you put an activation record, comprising the return address and all the local variable, on the stack. BASIC, on the other hand, usually manages only the return address and has gloabal variables only.
That is, I recently discovered that there’s an edge case, where 8-bit MS BASIC (at least in its Commodore variant) does have local variables, namely the argument for DEFined FN-functions. While this is a global variable, as well, the mechanism actually ignores the usual variable handling and a pointer in the FN-variable points directly to the address of the floating point value held by/in this variable. On call, the current content of these bytes is pushed onto the stack and restored again, as the function finishes. So this is a true local variable. – Meaning, probably you may come up with a true recursive subroutine combining GOSUB and FN()-calls?
Notably, you may call any FN-functions from within FN-functions. (While these are not recursive themselves, as they must return a finite value in a single statement – otherwise, you’ll end up in an infinite loop –, you may still utilize them with some external control logic in a GOSUB routine. But I don’t see a real application for this, as for any worthwhile tasks, you’d always need to manage some local state for any decisions and branching logic in a global variable.)
I once translated a solution I had initially written in Lisp recursively to Basic. I used the fact that GOSUBs did in fact nest and got around the lack of local variables by converting each variable into an array. So “last” became “last[sp]” and the subroutine would increment sp as the start and decrement it before returning.
The article I was responding to showed a Basic program to print all permutations of a number of elements. The author used nested FOR loops so needed a different version of the program for each number of elements. He claimed a more general solution was not possible in Basic which would contradict the Church-Turing thesis, so I sent in a program that proved otherwise.
It’s funny that the author was so close to being right. I remember the lectures on the Church-Turing thesis and the intuitive understanding was that fixed-limit FOR loops were not general enough but WHILE loops did all you need. FOR loops in the FORTRAN and BASIC sense, not C where they’re really WHILE loops in disguise.
So if the author only thought of using FOR loops then it’s true. But once you have IF and GOTO you can easily emulate WHILE. And you don’t even need GOSUB as you can emulate a call stack with an array just as you can emulate the local variable stack.
For those who like to split hairs I’ll do note that a BASIC FOR loop isn’t purely limited as a FOR K = 1 TO 2 STEP 0 will never terminate which gives it one essential feature of universality – the ability to loop indefinitely. And for practical purposes a FOR loop with a very large limit can be good enough for problems that fit into a machines available memory.
Similarly, you may manipulate the loop variable, possibly based on a decision (it’s not good style, but you can do that):
10 A=0
20 FOR I=0 TO 1
30 I=0 :REM LOOP FOREVER
40 GOSUB 1000
50 IF A<>0 THEN I=1 :REM LAST ITERATION
60 NEXT I
alternatively, provided that true is -1 and false is 0, which is really the same as DO…WHILE:
10 A=0:FOR I=-1 TO 0:GOSUB 1000:I=(A=0):NEXT
e.g., we may wait for a key-press like this (loop boundaries may depend on the implementation):
10 PRINT "PRESS ANY KEY..."
20 FOR I=-1 TO 0:GET K$:I=(K$=""):NEXT
30 PRINT "DONE."
And we may break out of loops, even nested ones, using a GOTO statement (which always kind of scared me, thinking of the interpreter having to pull the right values from the stack).
So the boundaries between WHILE and FOR-NEXT are quite fuzzy.
One thing to bear in mind is that the commonly used 6502 CPU had a pretty small stack, and 1980s era Microsoft BASIC on the Commodore 64 (and others) used the stack for GOSUB. Depending on your task, you could pretty quickly run out of stack space.
In practice, this was rarely a problem for most things. But if you were just really having fun experimenting with recursion, it could be an issue.
As for local variables, well … the most elegant solution is probably to fake it. You keep a STACK DEPTH variable, that you push +1 to whenever you start a subroutine, and you pop -1 from just before you RETURN. For each pseudo-local variable, you have an array and use SD as its index.
Basically, each pseudo-local variable array is its own fake stack.
(pun intended)
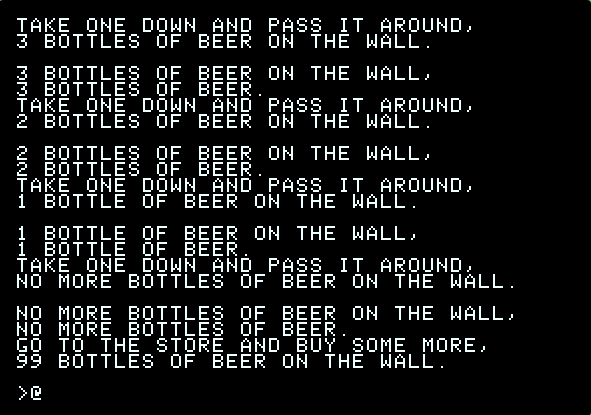
I don’t claim that this is the best way to do it, but I enjoyed myself toying with this Woz BASIC version of the classic programming exercise, with its quirky IF/THEN and FOR/NEXT (no WHILE/WEND):
40 FOR B=99 TO 98 STEP 0: PRINT : FOR W=0 TO 2: IF W<2 THEN 70
50 IF B THEN PRINT "TAKE ONE DOWN AND PASS IT AROUND";:B=B-1
60 IF B+1 THEN 70:B=99: PRINT "GO TO THE STORE AND BUY SOME MORE";
70 IF W THEN PRINT ",": IF B THEN PRINT B;: IF B=0 THEN PRINT "NO MORE";
80 PRINT " BOTTLE";: IF B-1 THEN PRINT "S";: PRINT " OF BEER";
90 IF W-1 THEN PRINT " ON THE WALL";: IF W THEN PRINT ".": NEXT W,B: END
If you try this verbatim in any other BASIC, it probably won’t error out, but it almost certainly will NOT produce the desired result.
OK. You got me thinking. So I wrote up a simple recursive program in BASIC.
10 I = 3
20 GOSUB 1000
30 END
1000 REM Subroutine
1010 IF I < 1 THEN RETURN
1020 PRINT "Before";I
1030 I = I - 1
1040 GOSUB 1000
1050 PRINT "After";I
1060 RETURN
It has the expected output of
Before 3
Before 2
Before 1
After 0
After 0
After 0
I tried this in GWBASIC, MBASIC on my Kaypro and on my Commodore PET 4032 with the same results.
So, strictly speaking, you can GOSUB from code that you GOSUBed to and you will return correctly.
Of course, the big problem in most BASICs is that all variables are global. So you can always replace this with a much simpler, and easier to understand, FOR loop.
So the question of “Did 80’s BASIC interpreters support recursion?” is “Yes”, but it’s pretty useless.
Like I said, you can fake local variables with arrays.
So, instead of I you could have DIM I(99) and you replace every instance of “I” with I(SD). You initialize SD to 0, and you add/subtract 1 to/from SD when you enter/exit the routine. Something like:
SD=0
DIM I(99)
…
GOSUB 1000
…
1000 SD=SD+1
… (use I(SD) instead of I in this code)
1060 SD=SD-1
1070 RETURN
To modify your example:
10 SD = 0
20 DIM I(99)
30 I(SD) = 3
40 GOSUB 1000
50 END
1000 REM Subroutine
1010 SD = SD + 1
1020 I(SD) = I(SD-1)
1030 IF I(SD) < 1 THEN GOTO 1080
1040 PRINT "BEFORE";I(SD)
1050 I(SD) = I(SD) - 1
1060 GOSUB 1000
1070 PRINT "AFTER";I(SD)
1080 SD = SD - 1
1090 RETURNOn a C64 the output is:
BEFORE 3
BEFORE 2
BEFORE 1
AFTER 0
AFTER 1
AFTER 2The ICL 2903E system installed in many UK colleges in the late 70s provided an interactive BASIC system written by North Staffordshire Polytechnic’s computer centre. It provided DEF FN with local variables and according to its users guide:
(see [Chapter four: Loops and branches — ICL CES - Computer Education in Schools])
40 DEF FNB (X, Y, Z$) A, P$
50 LET P$ = Z$ & Z$
60 LET A = LEN (P$)
70 ΙF Α > Χ + Υ ΤΗΕΝ 100
80 FNB = X + Y
90 GΟΤΟ 110
100 FNB = A
110 FNEND
.
.
400 REM FUNCTION CALL
410 LET Q = FNB (V, W, T$)
“It is possible to define a recursive function. See the 2903 BASIC: Reference manual for further information.”
Although I have a copy of the user guide, I’ve been unable to track down a copy of the reference manual.
I wonder if that was the system I used, at secondary school in North Staffs - we had a teletype connection to somewhere not too distant.
Ah, this site is perhaps your work? (It’s by a David…)
The system always announced itself something like this:
NSP 2903 BASIC SYSTEM
03/09/23 TIME 19:54:08
READY
I’m beginning to suspect I may own one of the few surviving copies of the ICL 2903 BASIC Users Guide. Although it has an ISBN, no UK copyright library seems to have it and I can’t find it mentioned in the archive of ICL material stored at the Science Museum in London. It was late being published and probably appeared in print for just one or two years before schools turned to micros.
I suspect the software used has been lost too.
I do hope you can scan it and share it - uploading to the internet archive is easy and safe (they will respond to any legitimate takedown request)