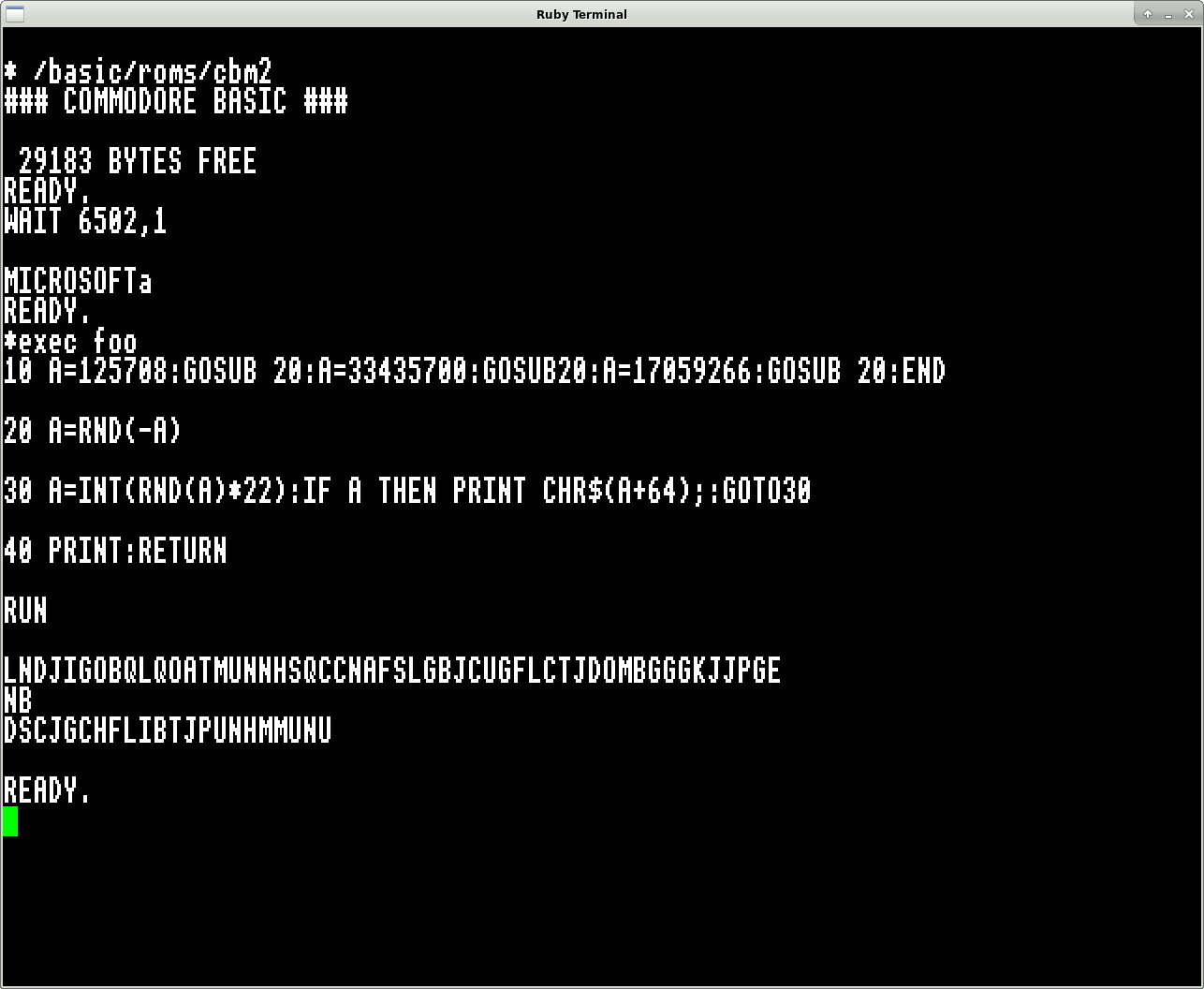
For anyone who wants to find another “secret message” in the C64 ROM:
If the argument of RND() is negative, we end up at the code at $E0D3, which just scrambles the argument. At this point, the argument is already in the floating point accumulator (FAC):
FAC:
0061 ... exponent
0062 ... mantissa 1
0063 ... mantissa 2
0064 ... mantissa 3
0065 ... mantissa 4
0066 ... extracted sign bit
0070 ... rounding bits
The code at $E0D3 swaps bytes 4 & 1, and bytes 2 & 3 of the mantissa and realigns the floating point value as a positive number between 0 and 1:
swap FAC mantissa 4 and 1
E0D3 LDX $65 X <- mantissa 4
E0D5 LDA $62 A <- mantissa 1
E0D7 STA $65 A -> mantissa 4
E0D9 STX $62 X -> mantissa 1
swap FAC mantissa 2 and 3
E0DB LDX $63 X <- mantissa 2
E0DD LDA $64 A <- mantissa 3
E0DF STA $63 A -> mantissa 2
E0E1 STX $64 X -> mantissa 3
clear sign of FAC (-> positive value)
E0E3 LDA #$00 load zero
E0E5 STA $66 store it as sign
handle exponent
E0E7 LDA $61 load FAC exponent
E0E9 STA $70 store it as rounding bits
(will be shifted in by NORMALIZE)
E0EB LDA #$80 load $80 (bias for exponent: value < 1)
E0ED STA $61 store it as FAC exponent
adjust and store return value
E0EF JSR $B8D7 call NORMALIZE (realign and clean up FAC)
E0F2 LDX #$8B set pointers for RND result
E0F4 LDY #$00 (RNDX: $008B)
E0F6 JMP $BBD4 round and store value of FAC there
Now reverse engineer your seed values…
(We’re still missing the code regarding how the rounding bits – containing the original exponent – are processed, but this is rather complex and lengthy. Maybe a blog post…)
Interestingly, the code for the PET ROM 1.0 looks identical, but doesn’t produce the same results (here, addresses align conveniently with the byte positions in FAC, starting at $B0 with the exponent, followed by the mantissa and the sign):
DF78 LDX $B4 swap mantissa 4 and 1
DF7A LDA $B1
DF7C STA $B4
DF7E STX $B1
DF80 LDX $B2 swap mantissa 2 and 3
DF82 LDA $B3
DF84 STA $B2
DF86 STX $B3
DF88 LDA #$00 clear sign
DF8A STA $B5
DF8C LDA $B0 load exponent
DF8E STA $BF store it as rounding bits
DF90 LDA #$80 set up new exponent
DF92 STA $B0
DF94 JSR $D7AC call NORMALIZE
DF97 LDX #$DA
DF99 LDY #$00 (RNDX: $00DA)
DF9B JMP $DAA6 copy result
The result is rather (as with PET BASIC 2/3 and 4):
LNDJIGOBQLQOATMUNNHSQCCNAFSLGBJCUGFLCTJDOMBGGGKJJPGE
NB
DSCJGCHFLIBTJPUNHMMUNU
Which suggests some differences in the floating point normalization? Maybe regarding rounding, where the original exponent is shifted in from the “rounding bits”?
(Again, an in-depth analysis is probably too lengthy for this thread.)