A discussion of floating point

Hardware
1

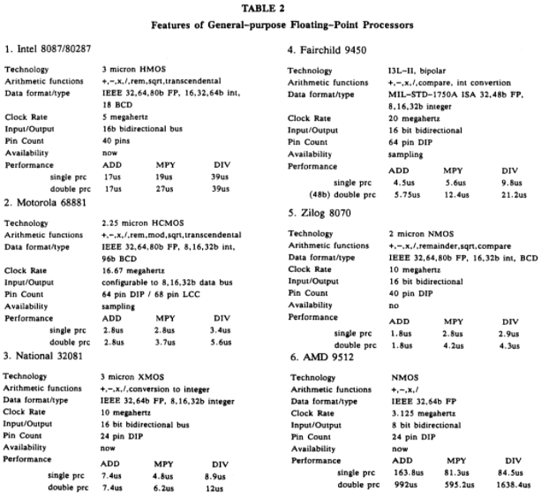
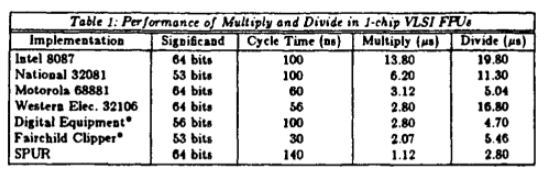
There is a very interesting discussion of floating point representations here:

https://groups.google.com/g/alt.folklore.computers/c/3YfodWFJCQc

The description is a little bit confusing, but it basically posits that there are two common layouts for floating point; both of them store the exponent and then the significand, but they differ in where they store the sign of the significand. Formats designed for hardware floating point tend to store the sign of the significand up front, while formats designed for software floating point tend to store the sign of the significand with the significand itself – presumably to make calculating the final value easier.

It seems that the original author has an interesting page on floating point numbers here, where he categorizes these two formats as “Group I” and “Group II”, and lists a truly staggering number of formats in visual form.

http://www.quadibloc.com/comp/cp0201.htm

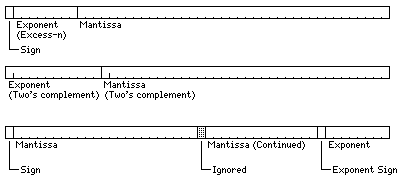
The Usenet discussion goes on to touch on quite a number of interesting historical formats, including some BCD and other “unusual” formats by modern lights.

An interesting note on floating point formats is that IEEE 754 seems to descend from the Digital PDP-10 format by way of the PDP-11 and then the Intel x87. The PDP-11 format is derived from the PDP-10, but the loss of four bits of space in the significand was felt keenly, so the designers introduced an implicit 1 bit on the significand (effectively giving it one more bit of precision, bringing it to 33 bits). Interestingly this required an exception in the format for the value zero (so that it could be represented as all zero bits), where that implicit 1 bit is an implicit zero. However, the PDP-11 (and the later VAX) did not take it farther than that exception. The x87 format (which was proposed by Intel and later became IEEE 754) used the resulting zero exponent as what is now termed a de-normalized value, which allows for “gradual underflow” in IEEE 754 terms; values very close to numeric zero are evenly spaced at the minimum spacing allowed by the length of the significand.

(The PDP-11 and VAX had another problem, which is that they were stored “stupid endian”, with little endian 16-bit words arranged in big-endian sequence; this is sometimes called “PDP-endian”, or even “NUXI”, for the order of the letters in the word UNIX stored in that format.)

3 Likes
2

(Some great things nearby on Quadibloc too!)

Nice notes about the PDP heritage there - thanks.

I’ve been mulling over floating point myself: I finally got the hang of the idea that exponentiation, particularly, needs more significand bits than the source or destination types, because logarithms in effect merge the exponent and significand. (Other calculations too, but that one is easy to grasp.) And so we get the 80 bit ‘extended precision’, invented for internal purposes but exposed to the programmer, with its 64 bits of significand.

And there was a time when FPUs generally offered extended precision: Motorola’s, for example. And GEC-Plessey’s for ARM. But with integrated FPUs and new instruction sets, we seem to be losing this offering.

Lots of interesting references to follow up on, in that Wikipedia article, including from William Kahan, who seems to have been a driving force.

Edit: nice comment in the linked usenet/groups thread:

IBM modified the 360 hardware to include a guard digit for floating-point.

Yes. That modification took place very shortly after the 360 was released, because it turned out that the behavior of FP without a guard digit on the initial machines was disastrous.

Even with the guard digit, with a hex exponent, and with truncation instead of rounding, IBM floating-point was not the greatest, and so care in numerical analysis was required with it. Of course, the Cray I was even worse, and the MANIAC II hardly bears thinking of.

2 Likes
3

At https://documents.epfl.ch/users/f/fr/froulet/www/HP/Algorithms.pdf, there’s a collection of articles about the algorithms used in HP calculators. Pretty interesting, and very different from how you would implement this on other types of hardware.

3 Likes
4

Nice find! Those, by William E Egbert, are from various 1977 issues of the HP Journal. Previously, in November 1976, we have Dennis W Harms explaining “The New Accuracy: making 2^3=8” describing the improvements made for the HP-91, as an enhancement of the algorithms seen in the HP-35.

5

Just to say a bit more on the adoption (or rejection) of the 80 bit ‘extended precision’ format, which has 64 bits of significand. In Computer Arithmetic: Volume II (ed. Earl E Swartzlander) we see these tables from mid-1980s papers:

image
image622×566 78.8 KB

image

which tell us that FPU chips from Intel, Zilog, Motorola, Western Electric, and the SPUR machine from UCB all offer 80 bit floats, whereas offerings from AMD, National, DEC, and Fairchild don’t.

1 Like
6

Whle the IBM 1130 was not around in the 80’s, I belive it had as a strange floating point option of 3 words.
32 bits fraction, 16 bits exponent. Floating point was software only.

7

I’ve often wondered why the exponent in IEEE 754 is biased instead of being 2’s complement. Sounds like it has something to do with ordering numbers. So smaller numbers are numerically lower when you treat the whole thing as an integer value. I’ll admit I don’t have a good grasp on how floating-point operations are performed.

Sort of related, the Quake III inverse square root algorithm

8

A good set of material here
https://www.computerhistory.org/collections/catalog/102639875

Dr Kahan also did an interview in IEEE March 1998, which he put the full version of rather than the magazine one at:

https://people.eecs.berkeley.edu/~wkahan/ieee754status/754story.html

It has some gems of quotes in it

“I have said from time to time, perhaps too cynically, that other Silicon Valley companies got worried enough to join a committee that might slow Intel down. It was the committee assembled to produce a standard for floating-point arithmetic on microprocessors.”

" My reasoning was based on the requirements of a mass market: A lot of code involving a little floating-point will be written by many people who have never attended my (nor anyone else’s) numerical analysis classes"

And here’s a fun little piece Joel Boney’s original Motorola 6800 floating point code (he went on to work on the standard and design the motorola FPU)

http://test.dankohn.info/~myhome/projects/68HC11/AXIOM_HC11/Source/Users%20Group/UG026

2 Likes
9

More 6800 floating point with friends

And a star trek game

1 Like
10

In this github issue (on a C toolchain for Z80) we see these comments and links:

I was wondering why AMD used a floating point format that was quite restrictive, and would have difficulty with extremely small or large scientific constants like Planck or Avogadro. Very poor planning, IMHO.

So I dug deeper and see that that the AMD developers were simply following the precedent set by the Lawrence Livermore Labs, with their 1975 Floating Point Library. [Edit: archived here.] And, even better, it turns out that some people still maintain this library (2015), and it is available as 8080 ASM code on Herb Johnson’s retro technology pages.

11

And hardware vanishes the next week or day. Floating Point Co-Processor uM-FPU v3.1 has come and gone. Spark fun once had them, other places perhaps.

12

Thanks for that one: it leads to a two hour video (“Floating Point - Past, present and Future”) featuring a number of presentations by significant figures(!) including Kahan at 1h20. Some good historical and technical information in there, although Kahan trails off into something of a bitter rant, about how much has been forgotten or ignored. He might be right of course. This is his paper corresponding to the talk. Here’s a snippet from the first presenter:

a lot of these meetings had run noon to midnight and we used to think the reason was that Dr Kahan could convince us of anything at midnight.

13

The direct link to the Livermore Labs 1975 Floating Point Library isn’t directly available anymore. There is a copy e.g. here: https://www.z80cpu.eu/files/archive/roche/171286.pdf
(and presumably on archive.org as well but I didn’t check - Edit: I see Ed found a good archive.org link)

Edit: GitHub - feilipu/LLL-Floating-Point: Floating-Point Package for Intel 8008 and 8080 Microprocessors has asm source.

1 Like
14

You won’t have any luck with those. Micromega Corporation was a one-man show, and when Cam Thompson passed away in 2015, there won’t be any more made. It was a pretty clever idea, using the floating point capabilities of a dsPIC micro-controller to provide mathematical grunt to smaller micro-controllers.

15

Nice little project though - 8 pin device, serially connected. Here’s a document.

There was a brief window in the 70s when electronics hobby magazines described projects to hook a calculator chip up to a micro. (Maybe a NatSemi offering?) Those chips are slow, but accurate, and the interfacing project is much simpler than a floating point software project. (That is, if it’s even possible to compare a software project with a hardware project!)

Edit: from 1977, a $45 product from SWTPC: MP-N Calculator

16

FWIW: I’m using the ATmega 1284p that’s the “host controller” in my Retro Ruby816 SBC (65c816 CPU) for floating point (and 32-bit MUL, DIV too) rather than code it natively in '816 assembler. Offloading the 32-bit MUL & DIV makes it faster than my naively coded ones too, however I could make the '816 code much faster with time & effort, but there’s that trade-off…

-Gordon

1 Like
17

Some hope.

1 Like
18

Nice chip on your side of the pond.Floating point conversion to and from ASCII is not often found
with a floating point device.

19

Thanks, Bobby, but I know that leads to a dead end. In 2017 I worked for a hobby electronics distributor, and we had a client who wanted a uM-FPU. I chased every lead on the web (including this one) but no-one had stock. We may have even tried contacting Mr Thompson’s widow since we were only a couple of hours away from where they lived. There were none in 2017, so there are even fewer in 2021.

Gordon - nice use of an ATMega!

1 Like
20

Would it be possible to get hold of his documents? Clone his work? Rabbit hole with no bottom?
Just curious after finding this thread.